3.1. Accelerating parallel code with PyCOMPSs and Numba

Demo Supercomputing 2019

What is mandelbrot?

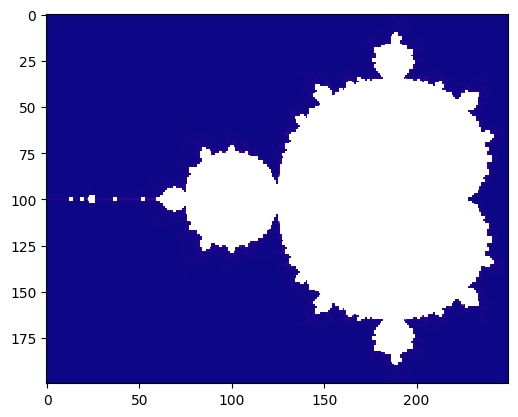
The mandelbrot set is a fractal, which is plotted on the complex plane. It shows how intrincate can be formed from a simple equation.

It is generated using the algorithm:

\begin{align} Z_{n+1} & = z_{n}^2 + A \\ \end{align}

Where Z and A are complex numbers, and n represents the number of iterations.

First, import time to measure the elapsed execution times and create an ordered dictionary to keep all measures -> we are going to measure and plot the performance with different conditions!

import time
from collections import OrderedDict
times = OrderedDict()

And then, all required imports

from numpy import NaN, arange, abs, array

Mandelbrot set implementation:

def mandelbrot(a, max_iter):
    z = 0
    for n in range(1, max_iter):
        z = z**2 + a
        if abs(z) > 2:
            return n
    return NaN

def mandelbrot_set(y, X, max_iter):
    Z = [0 for _ in range(len(X))]
    for ix, x in enumerate(X):
        Z[ix] = mandelbrot(x + 1j * y, max_iter)
    return Z

Main function to generate the mandelbrot set. It splits the space in vertical chunks, and calculates the mandelbrot set of each one, generating the result Z.

def run_mandelbrot(X, Y, max_iter):
    st = time.time()
    Z = [[] for _ in range(len(Y))]
    for iy, y in enumerate(Y):
        Z[iy] = mandelbrot_set(y, X, max_iter)
    elapsed = time.time() - st
    print("Elapsed time (s): {}".format(elapsed))
    return Z, elapsed

The following function plots the fractal inline (the coerced parameter <Boolean> is used to set NaN in coerced elements within Z).

%matplotlib inline
def plot_fractal(Z, coerced):
    if coerced:
        Z = [[NaN if c == -2**63 else c for c in row] for row in Z]
    import matplotlib.pyplot as plt
    Z = array(Z)
    plt.imshow(Z, cmap='plasma')
    plt.show()

Define a benchmarking function:

def generate_fractal(coerced=False):
    X = arange(-2, .5, .01)
    Y = arange(-1.0,  1.0, .01)
    max_iterations = 2000
    Z, elapsed = run_mandelbrot(X, Y, max_iterations)
    plot_fractal(Z, coerced)
    return elapsed

Run the previous code sequentially:

times['Sequential'] = generate_fractal()

Elapsed time (s): 34.20736598968506

Paralellization with PyCOMPSs

After analysing the code, each mandelbrot set can be considered as a task, requiring only to decorate the mandelbrot_set function. It is interesting to observe that all sets are independent among them, so they can be computed completely independently, enabling to exploit multiple resources concurrently.

In order to run this code with we need first to start the COMPSs runtime:

import os
import pycompss.interactive as ipycompss
if 'BINDER_SERVICE_HOST' in os.environ:
    ipycompss.start(project_xml='../xml/project.xml',
                    resources_xml='../xml/resources.xml')
else:
    ipycompss.start(project_xml='./project.xml',
                    resources_xml='./resources.xml',
                    graph=False, trace=True, monitor=1000)

********************************************************
**************** PyCOMPSs Interactive ******************
********************************************************
*          .-~~-.--.           ______         ______   *
*         :         )         |____  \       |____  \  *
*   .~ ~ -.\       /.- ~~ .      __) |          __) |  *
*   >       `.   .'       <     |__  |         |__  |  *
*  (         .- -.         )   ____) |   _    ____) |  *
*   `- -.-~  `- -'  ~-.- -'   |______/  |_|  |______/  *
*     (        :        )           _ _ .-:            *
*      ~--.    :    .--~        .-~  .-~  }            *
*          ~-.-^-.-~ \_      .~  .-~   .~              *
*                   \ \ '     \ '_ _ -~                *
*                    \`.\`.    //                      *
*           . - ~ ~-.__\`.\`-.//                       *
*       .-~   . - ~  }~ ~ ~-.~-.                       *
*     .' .-~      .-~       :/~-.~-./:                 *
*    /_~_ _ . - ~                 ~-.~-._              *
*                                     ~-.<             *
********************************************************
* - Starting COMPSs runtime...                         *
* - Log path : /home/user/.COMPSs/Interactive_23/
* - PyCOMPSs Runtime started... Have fun!              *
********************************************************

It is necessary to decorate the mandelbrot_set function with the @task decorator.

Note that the mandelbrot_set function returns a list of elements.

from pycompss.api.task import task

@task(returns=list)
def mandelbrot_set(y, X, max_iter):
    Z = [0 for _ in range(len(X))]
    for ix, x in enumerate(X):
        Z[ix] = mandelbrot(x + 1j * y, max_iter)
    return Z

And finally, include the synchronization of Z with compss_wait_on.

from pycompss.api.api import compss_wait_on

def run_mandelbrot(X, Y, max_iter):
    st = time.time()
    Z = [[] for _ in range(len(Y))]
    for iy, y in enumerate(Y):
        Z[iy] = mandelbrot_set(y, X, max_iter)
    Z = compss_wait_on(Z)
    elapsed = time.time() - st
    print("Elapsed time (s): {}".format(elapsed))
    return Z, elapsed

Run the benchmark with PyCOMPSs:

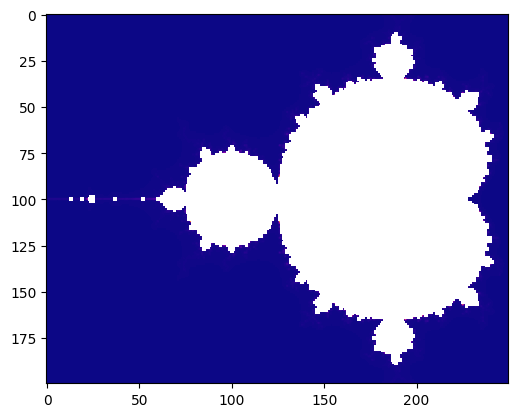
times['PyCOMPSs'] = generate_fractal()

Found task: mandelbrot_set
Elapsed time (s): 20.21534013748169

Accelerating the tasks with Numba

To this end, it is necessary to either use: 1. the Numba’s @jit decorator under the PyCOMPSs @task decorator 2. or define the numba=True within the @task decorator.

First, we decorate the inner function (mandelbrot) with @jit since it is also a target function to be optimized with Numba.

from numba import jit

@jit(nopython=True)
def mandelbrot(a, max_iter):
    z = 0
    for n in range(1, max_iter):
        z = z**2 + a
        if abs(z) > 2:
            return n
    return NaN # NaN is coerced by Numba

Option 1 - Add the @jit decorator explicitly under @task decorator

@task(returns=list) @jit def mandelbrot_set(y, X, max_iter): Z = [0 for _ in range(len(X))] for ix, x in enumerate(X): Z[ix] = mandelbrot(x + 1j * y, max_iter) return Z

Option 2 - Add the numba=True flag within @task decorator

@task(returns=list, numba=True)
def mandelbrot_set(y, X, max_iter):
    Z = [0 for _ in range(len(X))]
    for ix, x in enumerate(X):
        Z[ix] = mandelbrot(x + 1j * y, max_iter)
    return Z

Run the benchmark with Numba:

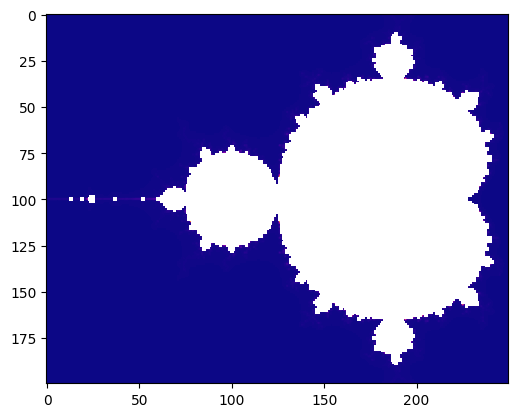
times['PyCOMPSs + Numba'] = generate_fractal(coerced=True)

Found task: mandelbrot_set
Elapsed time (s): 15.769368648529053

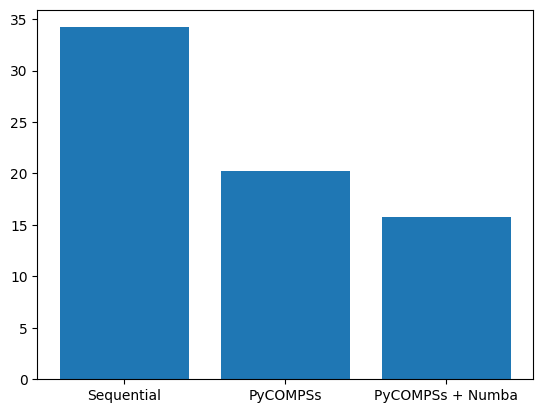
Plot the times:

import matplotlib.pyplot as plt
plt.bar(*zip(*times.items()))
plt.show()

Stop COMPSs runtime

ipycompss.stop()

********************************************************
***************** STOPPING PyCOMPSs ********************
********************************************************
Checking if any issue happened.
Warning: some of the variables used with PyCOMPSs may
         have not been brought to the master.
********************************************************