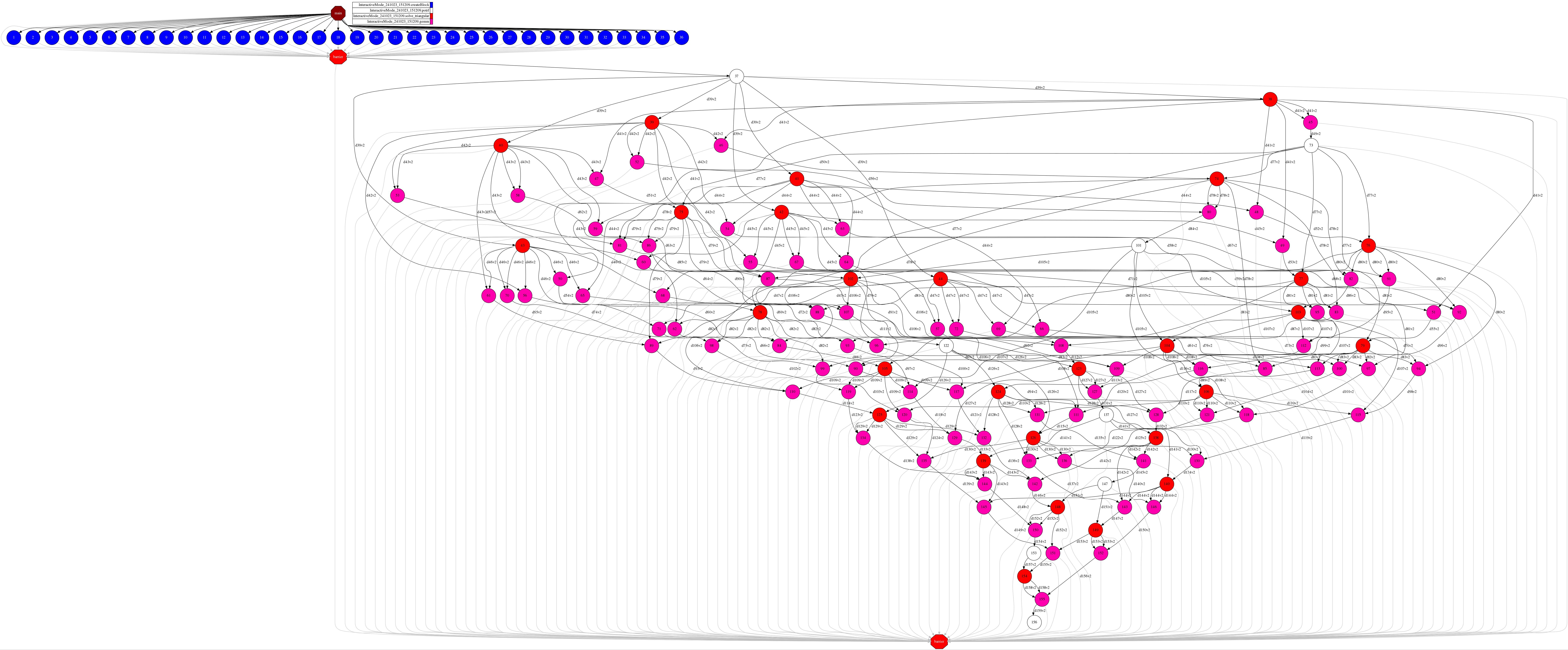
2.4. Cholesky Decomposition/Factorization
Given a symmetric positive definite matrix A, the Cholesky decomposition is an upper triangular matrix U (with strictly positive diagonal entries) such that:
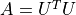
[1]:
import pycompss.interactive as ipycompss
[2]:
# Start PyCOMPSs runtime with graph and tracing enabled
import os
if 'BINDER_SERVICE_HOST' in os.environ:
ipycompss.start(graph=True, trace=True,
project_xml='../xml/project.xml',
resources_xml='../xml/resources.xml')
else:
ipycompss.start(graph=True, monitor=1000, trace=True)
********************************************************
**************** PyCOMPSs Interactive ******************
********************************************************
* .-~~-.--. ______ ______ *
* : ) |____ \ |____ \ *
* .~ ~ -.\ /.- ~~ . __) | __) | *
* > `. .' < |__ | |__ | *
* ( .- -. ) ____) | _ ____) | *
* `- -.-~ `- -' ~-.- -' |______/ |_| |______/ *
* ( : ) _ _ .-: *
* ~--. : .--~ .-~ .-~ } *
* ~-.-^-.-~ \_ .~ .-~ .~ *
* \ \ ' \ '_ _ -~ *
* \`.\`. // *
* . - ~ ~-.__\`.\`-.// *
* .-~ . - ~ }~ ~ ~-.~-. *
* .' .-~ .-~ :/~-.~-./: *
* /_~_ _ . - ~ ~-.~-._ *
* ~-.< *
********************************************************
* - Starting COMPSs runtime... *
* - Log path : /home/user/.COMPSs/Interactive_18/
* - PyCOMPSs Runtime started... Have fun! *
********************************************************
[3]:
from pycompss.api.task import task
from scipy import linalg
import numpy as np
import ctypes
Task definitions
[4]:
@task(returns=list)
def createBlock(BSIZE, MKLProc, diag):
import os
os.environ["MKL_NUM_THREADS"]=str(MKLProc)
block = np.array(np.random.random((BSIZE, BSIZE)), dtype=np.double,copy=False)
mb = np.matrix(block, dtype=np.double, copy=False)
mb = mb + np.transpose(mb)
if diag:
mb = mb + 2*BSIZE*np.eye(BSIZE)
return mb
@task(returns=np.ndarray)
def potrf(A, MKLProc):
from scipy.linalg.lapack import dpotrf
import os
os.environ['MKL_NUM_THREADS']=str(MKLProc)
A = dpotrf(A, lower=True)[0]
return A
@task(returns=np.ndarray)
def solve_triangular(A, B, MKLProc):
from scipy.linalg import solve_triangular
from numpy import transpose
import os
os.environ['MKL_NUM_THREADS']=str(MKLProc)
B = transpose(B)
B = solve_triangular(A, B, lower=True) # , trans='T'
B = transpose(B)
return B
@task(returns=np.ndarray)
def gemm(alpha, A, B, C, beta, MKLProc):
from scipy.linalg.blas import dgemm
from numpy import transpose
import os
os.environ['MKL_NUM_THREADS']=str(MKLProc)
B = transpose(B)
C = dgemm(alpha, A, B, c=C, beta=beta)
return C
Auxiliar functions
[5]:
def genMatrix(MSIZE, BSIZE, MKLProc, A):
for i in range(MSIZE):
A.append([])
for j in range(MSIZE):
A[i].append([])
for i in range(MSIZE):
mb = createBlock(BSIZE, MKLProc, True)
A[i][i]=mb
for j in range(i+1,MSIZE):
mb = createBlock(BSIZE, MKLProc, False)
A[i][j]=mb
A[j][i]=mb
[6]:
def cholesky_blocked(MSIZE, BSIZE, mkl_threads, A):
import os
for k in range(MSIZE):
# Diagonal block factorization
A[k][k] = potrf(A[k][k], mkl_threads)
# Triangular systems
for i in range(k+1, MSIZE):
A[i][k] = solve_triangular(A[k][k], A[i][k], mkl_threads)
A[k][i] = np.zeros((BSIZE,BSIZE))
# update trailing matrix
for i in range(k+1, MSIZE):
for j in range(i, MSIZE):
A[j][i] = gemm(-1.0, A[j][k], A[i][k], A[j][i], 1.0, mkl_threads)
return A
MAIN Code
Parameters (that can be configured in the following cell): * MSIZE: Matrix size (default: 8) * BSIZE: Block size (default: 1024) * mkl_threads: Number of MKL threads (default: 1)
[7]:
import ipywidgets as widgets
from pycompss.api.api import compss_barrier
import time
w_MSIZE = widgets.IntText(value=8)
w_BSIZE = widgets.IntText(value=1024)
w_mkl_threads = widgets.IntText(value=1)
def cholesky(MSIZE, BSIZE, mkl_threads):
# Generate de matrix
startTime = time.time()
# Generate supermatrix
A = []
res = []
genMatrix(MSIZE, BSIZE, mkl_threads, A)
compss_barrier()
initTime = time.time() - startTime
startDecompTime = time.time()
res = cholesky_blocked(MSIZE, BSIZE, mkl_threads, A)
compss_barrier()
decompTime = time.time() - startDecompTime
totalTime = decompTime + initTime
print("---------- Elapsed Times ----------")
print("initT:{}".format(initTime))
print("decompT:{}".format(decompTime))
print("totalTime:{}".format(totalTime))
print("-----------------------------------")
widgets.interact_manual(cholesky, MSIZE=w_MSIZE, BSIZE=w_BSIZE, mkl_threads=w_mkl_threads)
[7]:
<function __main__.cholesky(MSIZE, BSIZE, mkl_threads)>
[8]:
ipycompss.stop()
********************************************************
***************** STOPPING PyCOMPSs ********************
********************************************************
Checking if any issue happened.
Warning: some of the variables used with PyCOMPSs may
have not been brought to the master.
********************************************************
[9]:
ipycompss.complete_task_graph(fit=True)